Никифоров Кирилл
Никифоров Кирилл
Запишем разложение бинома (1 – 2 * a)^6.
(1 – 2 * a)^6;
(1 – 2 * a)^2 * (1 – 2 * a)^2 * (1 – 2 * a)^2;
(1 – 2 * 1 * 2 * a + (2 * a)^2) * (1 – 2 * a)^2 * (1 – 2 * a)^2;
(1 – 4 * a + 4 * a^2) * (1 – 4 * a + 4 * a^2) * (1 – 4 * a + 4 * a^2);
(1 – 4 * a + 4 * a^2)^3;
((1 – 4 * a) + (4 * a^2))^3;
(1 – 4 * a)^3 – 3 * (1 – 4 * a)^2 * 4 * a^2 + 3 * (1 – 4 * a) * (4 * a^2)^2 – (4 * a^2)^3;
1 – 12 * a + 48 * a^2 – 64 * a^3 – 12 * a^2 * (1 – 8 * a + 16 * a^2) – 48 * a^4 * (1 – 4 * a) – 64 * a^6;
1 – 12 * a + 48 * a^2 – 64 * a^3 – 12 * a^2 + 96 * a^3 – 192 * a^4 – 48 * a^4 + 192 * a^4 – 64 * a^6;
1 – 12 * a + 36 * a^2 + 32 * a^3 – 48 * a^4 – 64 * a^6.
Пожаловаться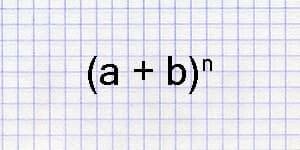 Теги:КомбинаторикаФормула бинома Ньютона позволяет разложить двучлен вида (a+b)n в многочлен от a и b. Общая формула выглядит так: (a + b)n = an + Сn1 · an – 1 · b + Сn2 · an – 2 · b2 + … + Сnk · an – k · bk + … + Сnn – 1 · a · bn-1 + bn, где С – биномиальные коэффициенты, которые определяются через треугольник Паскаля. Важное свойство треугольника Паскаля: каждое число равно сумме двух чисел, стоящих над ним.
Теги:КомбинаторикаФормула бинома Ньютона позволяет разложить двучлен вида (a+b)n в многочлен от a и b. Общая формула выглядит так: (a + b)n = an + Сn1 · an – 1 · b + Сn2 · an – 2 · b2 + … + Сnk · an – k · bk + … + Сnn – 1 · a · bn-1 + bn, где С – биномиальные коэффициенты, которые определяются через треугольник Паскаля. Важное свойство треугольника Паскаля: каждое число равно сумме двух чисел, стоящих над ним.
Формула Бинома Ньютона
Для натурального n формула принимает такой вид:
(a + b)n = Cn · an + C1n · an-1 · b + C2n · an-2 · b2 + … + Cn-1n · a · bn-1 + Cnn · bn,
где Ckn – биномиальные коэффициенты.
Примеры:
- (x + y)2 = x2 + 2 · x · y + y2,
- (x + y)3 = x3 + 3 · x2 · y + 3 · x · y2 + y3,
- (x + y)4 = x4 + 4 · x3 · y + 6 · x2 · y2 + 4 · x · y3 + y4,
- (x + y)5 = x5 + 5 · x4 · y + 10 · x3 · y2 + 10 · x2 · y3 + 5 · x · y4 + y5,
Треугольник Паскаля
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, которые для удобства восприятия записаны в форме треугольника. На его вершинах и по боковым сторонам стоят единицы, а каждое число равно сумме двух чисел над ним.
Скопировать «Разложение Бинома Ньютона»:
Код для вставки:
Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился сервис транслитерации.
Добавить в закладки:
Комментарии к калькулятору
Количество комментариев: 3Похожие калькуляторыМатематикаЧисло перестановок
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Перейти к расчетуМатематикаЧисло сочетаний
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Перейти к расчетуМатематикаЧисло размещений
Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.
Перейти к расчетуОтветы (1)Знаешь ответ?Не уверен в ответе? Найди верный ответ на вопрос ✅ «Записать разложение бинома: 1) (a-2b) в 6 степени 2) (1+2x) в 5 степени …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов. Новые вопросы по алгебреНайдите значение выражения корень 0,081 корень 0,9Ответы (1)Решите рациональное уранение используя равносильные преобразования √2x-3+√4x+1=4Ответы (1)Два автобиля двигались на встречу к друг другу. Через. 2 ч после встречи, пасстояние между ними стало равным 280 ум. найдите скорость автомобилей., еслт у одного из них скорость меньше на 10/км. чОтветы (1)Найдите корень уравнения (2x-1) ^2-4x^2Ответы (1)Не строя график функции y=-0,3x+2 выяснить, принадлежит ли графику точки M (3; 1,1) K (-5; 3,5)Ответы (1)Используемые источники:
- https://vashurok.ru/questions/zapishite-razlozhenie-binoma-1-2a-6
- https://poformule.ru/matematika/razlozhenie-binoma-nyutona
- https://urokam.net/algebra/589024.html
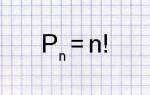 Бином Ньютона.
Бином Ньютона.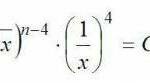 Калькулятор разложения Бинома Ньютона
Калькулятор разложения Бинома Ньютона