Содержание
| 13:39 Разложение бинома ньютона онлайн |
|
Пример 1. Найти разложение степени бинома (2x–3)5? Решение. Смотри формулу бинома Ньютона свойства сочетаний Полагая a=2x, b=–3, получим
Проверить разложение можно с помощью калькулятора: $left ( sqrt[3]{x} +frac{1}{x} right )^{n}$ не зависит от x. Найти n. Решение. Пятый член разложения T5 имеет следующий вид:
По условию T5 не зависит от x; это означает, что показатель степени при x равен нулю, т.е. (n–4)/3–4=0. Из последнего уравнения находим n=16. Задачи. 1.34. Имеется 12 различных цветов. Сколькими способами можно составить букет из данных цветов, если в букет должно входить не менее 3 цветов? а) (x+1)7; б) (x-2)5; в) (3x+2y)4. Найдите: а) биномиальный коэффициент среднего члена разложение (a+b)20; б) четвертый член разложения (8x–5y)6. 1.37. Сумма биномиальных коэффициентов разложения $left ( frac{2x}{3} +frac{3}{2nx^2} right )^{n}$ равна 64. Напишите член, не содержащий переменную 1.38. Сумма третьего от начала и третьего от конца биномиальных коэффициентов разложения $left (sqrt[4]{3} +sqrt[3]{4} right )^{n}$ равна 9900. Сколько рациональных членов содержится в этом разложении? |
| –>Категория–>:Комбинаторика | –>Просмотров–>:112545 | | | |
| –>Всего комментариев–>: 3 |
| <label>Порядок вывода комментариев:</label> |
–>
Теги:КомбинаторикаФормула бинома Ньютона позволяет разложить двучлен вида (a+b)n в многочлен от a и b. Общая формула выглядит так: (a + b)n = an + Сn1 · an – 1 · b + Сn2 · an – 2 · b2 + … + Сnk · an – k · bk + … + Сnn – 1 · a · bn-1 + bn, где С – биномиальные коэффициенты, которые определяются через треугольник Паскаля. Важное свойство треугольника Паскаля: каждое число равно сумме двух чисел, стоящих над ним.
Формула Бинома Ньютона
Для натурального n формула принимает такой вид:
(a + b)n = Cn · an + C1n · an-1 · b + C2n · an-2 · b2 + … + Cn-1n · a · bn-1 + Cnn · bn,
где Ckn – биномиальные коэффициенты.
Примеры:
- (x + y)2 = x2 + 2 · x · y + y2,
- (x + y)3 = x3 + 3 · x2 · y + 3 · x · y2 + y3,
- (x + y)4 = x4 + 4 · x3 · y + 6 · x2 · y2 + 4 · x · y3 + y4,
- (x + y)5 = x5 + 5 · x4 · y + 10 · x3 · y2 + 10 · x2 · y3 + 5 · x · y4 + y5,
Треугольник Паскаля
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, которые для удобства восприятия записаны в форме треугольника. На его вершинах и по боковым сторонам стоят единицы, а каждое число равно сумме двух чисел над ним.
Скопировать «Разложение Бинома Ньютона»:
Код для вставки:
Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился сервис транслитерации.
Добавить в закладки:
Комментарии к калькулятору
Количество комментариев: 3Похожие калькуляторыМатематикаЧисло перестановок
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Перейти к расчетуМатематикаЧисло сочетаний
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Перейти к расчетуМатематикаЧисло размещений
Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.
Перейти к расчету
Бином представляет собой выражение, которое состоит из двух одночленов. Биномиальные уравнения — равенства, которые содержат два члена в любой степени.
Определение термина
Моном — выражение вида axn, при этом переменных может быть больше одной. Например, к мономам относятся выражения 5x3, 4xy2 или 12xyz3. Бином — это выражение, которое состоит из двух мономов. Следовательно, это может быть, как 5x3 + 4xy2, так и 2x + 1. Последний представляет собой линейный бином, который в общем виде записывается как ax + b.
Бином Ньютона
Бином Ньютона — это формула разложения на слагаемые произведения вида (a+b)n, в результате чего всегда образуется полином. Если показатель степени n меньше 3 включительно, то выражение раскладывается по формулам сокращенного умножения, таким как квадрат и куб суммы/разности. Для степеней выше 3 формула разложения значительно усложняется, как и количество мономов, входящих в результирующий многочлен. Для упрощения поиска коэффициентов используется треугольник Паскаля, в котором номер строки совпадает со степенью произведения.
Биномиальные уравнения
Биномиальное уравнение — это равенство, которое содержит в себе два члена. Наиболее простыми биномиальными равенствами считаются линейные, которые в общем виде записываются как aZ+b. Более сложные биномиальные равенства могут содержать несколько переменных с разными степенями. В этой статье мы рассмотрим алгоритм умножения двух линейных биномиальных уравнений.
Алгоритм умножения
Произведение двух биномиальных равенств в общем виде записывается как:
(aZ+b) × (cZ + d),
где Z — неизвестное, a, b, c, d — числа.
Умножение многочлена на многочлен производится по стандартному правилу: каждый член первого полинома умножается на каждый член второго полинома, после чего мономы складываются и приводятся подобные. На практике это выглядит следующим образом:
- умножим первый член бинома (aZ+b) на каждый член бинома (cZ + d) и получим aZ × cZ + aZ × d =acZ2 + adZ;
- умножим второй член первого бинома на каждый член второго и получим b × cZ + b × d = bcZ + bd;
- суммируем все составляющие и запишем результат acZ2 + adZ + bcZ + bd.
Числовые значения в конкретных примерах всегда вычисляются, поэтому мы легко можем привести подобные и принять, что сумма adZ + bcZ = BZ. Остальные числовые произведения также вычисляются и заменяются большими буквами acZ2 = AZ2 и bd = C. Таким образом, в результате мы получаем полином вида:
AZ2 + BZ + C.
Если же бином возводится в квадрат, то легко применить сокращенную формулу умножения квадрат/разность суммы и получить тот же самый результат.
Калькулятор умножения двух биномиальных уравнений
Наша программа представляет собой онлайн-калькулятор для умножения двух линейных биномиальных уравнений. Для поиска решения требуется ввести коэффициенты уравнений, после чего программа вычислит результирующий квадратный полином. Рассмотрим пример работы инструмента.
Проверка корней
Калькулятор легко использовать для проверки корней квадратных уравнений. Если при решении уравнения вида AZ2 + BZ + C были получены целочисленные корни X1 и X2, то в результате умножения биномов вида (Z − X1) × (Z − X2) мы вновь получим выражение AZ2 + BZ + C. Например, есть уравнение:
x2 − 8x + 15 = 0
При решении через дискриминант мы получаем два корня X1 = 3 и X2 = 5. Для проверки решения введите в ячейку при X единицы, а в ячейки свободных членов — минус 3 и минус 5. В результате мы получим (1x2 − 5x − 3x + 15) = 1x2 − 8x + 15. Обратите внимание, что в произведении биномов корни требуется вычитать, поэтому если корни уравнений будут отрицательными, их знак изменится на плюс.
Заключение
Умножение биномиальных уравнений используется при упрощении выражений в самых разных расчетах, а также для проверки корней квадратных уравнений. Наш сервис позволяет мгновенно умножить два линейных биноминальных уравнения и получить в результате квадратичное равенство. Используйте программы из нашего каталога для решения любых математических задач.
Биноминальное разложение с использованием треугольника Паскаля
Рассмотрим следующие выражения со степенями (a + b)n, где a + b есть любой бином, а n – целое число. Каждое выражение – это полином. Во всех выражениях можно заметить особенности.
1. В каждом выражении на одно слагаемое больше, чем показатель степени n.
2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.
3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.
4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до “половины пути”, а потом уменьшаются на те же значения обратно к 1.
Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти значение (a + b)6. Согласно особенности, которую мы только что заметили, здесь должно быть 7 членовa6 + c1a5b + c2a4b2 + c3a3b3 + c4a2b4 + c5ab5 + b6. Но как мы можем определить значение каждого коэффициента, ci? Мы можем сделать это двумя путями. Первый метод включает в себя написание коэффициентов треугольником, как показано ниже. Это известно как Треугольник Паскаля:Есть много особенностей в треугольнике. Найдите столько, сколько сможете.Возможно вы нашли путь, как записать следующую строку чисел, используя числа в строке выше. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b)6 путем добавления следующей строки, используя особенности, которые мы нашли: Мы видим, что в последней строке
первой и последнее числа 1; второе число равно 1 + 5, или 6;третье число это 5 + 10, или 15;четвертое число это 10 + 10, или 20;пятое число это 10 + 5, или 15; ишестое число это 5 + 1, или 6.
Таким образом, выражение (a + b)6 будет равно(a + b)6 = 1a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + 1b6.
Для того, чтобы возвести в степень (a + b)8, мы дополняем две строки к треугольнику Паскаля:Тогда (a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Мы можем обобщить наши результаты следующим образом.
Бином Ньютона с использованием треугольника Паскаля
Для любого бинома a+ b и любого натурального числа n,(a + b)n = canb + c1an-1b1 + c2an-2b2 + …. + cn-1a1bn-1 + cnabn,где числа c, c1, c2,…., cn-1, cn взяты с (n + 1) ряда треугольника Паскаля.
Пример 1 Возведите в степень: (u – v)5.
Решение У нас есть (a + b)n, где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:1 5 10 10 5 1Тогда у нас есть(u – v)5 = [u + (-v)]5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 – 5u4v + 10u3v2 – 10u2v3 + 5uv4 – v5. Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.
Пример 2 Возведите в степень: (2t + 3/t)4.
Решение У нас есть (a + b)n, где a = 2t, b = 3/t, и n = 4. Мы используем 5-й ряд треугольника Паскаля:1 4 6 4 1Тогда мы имеем
Разложение бинома используя значения факториала
Предположим, что мы хотим найти значение (a + b)11. Недостаток в использовании треугольника Паскаля в том, что мы должны вычислить все предыдущие строки треугольника, чтобы получить необходимый ряд. Следующий метод позволяет избежать этого. Он также позволяет найти определенную строку – скажем, 8-ю строку – без вычисления всех других строк. Этот метод полезен в вычислениях, статистике и он использует биномиальное обозначение коэффициента.Мы можем сформулировать бином Ньютона следующим образом.
Бином Ньютона с использованием обозначение факториала
Для любого бинома (a + b) и любого натурального числа n,.
Бином Ньютона может быть доказан методом математической индукции. Она показывает почему называется биноминальным коэффициентом.
Пример 3 Возведите в степень: (x2 – 2y)5.
Решение У нас есть (a + b)n, где a = x2, b = -2y, и n = 5. Тогда, используя бином Ньютона, мы имеем Наконец, (x2 – 2y)5 = x10 – 10x8y + 40x6y2 – 80x4y3 + 80x2y4 – 35y5.
Пример 4 Возведите в степень: (2/x + 3√x)4.
Решение У нас есть (a + b)n, где a = 2/x, b = 3√x, и n = 4. Тогда, используя бином Ньютона, мы получимFinally (2/x + 3√x)4 = 16/x4 + 96/x5/2 + 216/x + 216x1/2 + 81x2.
Нахождение определенного члена
Предположим, что мы хотим определить тот или иной член термин из выражения. Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.
Обратите внимание, что в биноме Ньютона дает нам 1-й член, дает нам 2-й член, дает нам 3-й член и так далее. Это может быть обощено следующим образом.
Нахождение (k + 1) члена
(k + 1) член выражения (a + b)n есть .
Пример 5 Найдите 5-й член в выражении (2x – 5y)6.
Решение Во-первых, отмечаем, что 5 = 4 + 1. Тогда k = 4, a = 2x, b = -5y, и n = 6. Тогда 5-й член выражения будет
Пример 6 Найдите 8-й член в выражении (3x – 2)10.
Решение Во-первых, отмечаем, что 8 = 7 + 1. Тогда k = 7, a = 3x, b = -2 и n = 10. Тогда 8-й член выражения будет
Общее число подмножеств
Предположим, что множество имеет n объектов. Число подмножеств, содержащих k элементов есть . Общее число подмножеств множества есть число подмножеств с 0 элементами, а также число подмножеств с 1 элементом, а также число подмножеств с 2-мя элементами и так далее. Общее число подмножеств множества с n элементами есть .Теперь давайте рассмотрим возведение в степень (1 + 1)n:. Так. общее количество подмножеств (1 + 1)n, или 2n. Мы доказали следующее.
Полное число подмножеств
Полное число подмножеств множества с n элементами равно 2n.
Пример 7 Сколько подмножеств имеет множество {A, B, C, D, E}?
Решение Множество имеет 5 элементов, тогда число подмножеств равно 25, или 32.
Пример 8 Сеть ресторанов Венди предлагает следующую начинку для гамбургеров:{кетчуп, горчица, майонез, помидоры, салат, лук, грибы, оливки, сыр}.Сколько разных видов гамбургеров может предложить Венди, исключая размеры гамбургеров или их количество?
Решение Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно . Таким образом, Венди может предложить 512 различных гамбургеров.
Используемые источники:
- http://www.reshim.su/blog/razlozhenie_binoma_njutona_onlajn/2015-08-03-574
- https://poformule.ru/matematika/razlozhenie-binoma-nyutona
- https://bbf.ru/calculators/183/
- https://www.math10.com/ru/algebra/veroiatnosti/binominalnaya-teorema/binominalnaya-teorema.html
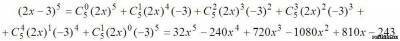
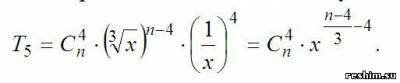 .
.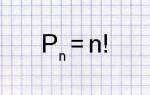 Бином Ньютона.
Бином Ньютона. САЙТ ИЗДАТЕЛЬСТВА БИНОМ
САЙТ ИЗДАТЕЛЬСТВА БИНОМ